ENMA: Tokenwise Autoregression for Generative Neural PDE Operators.
2 Criteo AI Lab, Paris, France
* Equal contribution.
Solving time-dependent parametric partial differential equations (PDEs) remains a fundamental challenge for neural solvers, particularly when generalizing across a wide range of physical parameters and dynamics. When data is uncertain or incomplete—as is often the case—a natural approach is to turn to generative models.We introduce ENMA, a generative neural operator designed to model spatio-temporal dynamics arising from physical phenomena. ENMA predicts future dynamics in a compressed latent space using a generative masked autoregressive transformer trained with flow matching loss, enabling tokenwise generation. Irregularly sampled spatial observations are encoded into uniform latent representations via attention mechanisms and further compressed through a spatio-temporal convolutional encoder. This allows ENMA to perform in-context learning at inference time by conditioning on either past states of the target trajectory or auxiliary context trajectories with similar dynamics. The result is a robust and adaptable framework that generalizes to new PDE regimes and supports one-shot surrogate modeling of time-dependent parametric PDEs.
We introduce ENMA (presented in the Figure below), a continuous autoregressive neural operator for modeling time-dependent parametric PDEs, where parameters such as initial conditions, coefficients, and forcing terms may vary across instances. ENMA operates entirely in a continuous latent space and advances both the encoder-decoder pipeline and the generative modeling component crucial to neural PDE solvers. The encoder employs attention mechanisms to process irregular spatio-temporal inputs (i.e., unordered point sets) and maps them onto a structured, grid-aligned latent space. A causal spatio-temporal convolutional encoder then compresses these observations into compact latent tokens spanning multiple states. Generation proceeds in two stages. A causal transformer first predicts future latent states autoregressively. Then, a masked spatial transformer decodes each state at the token level using Flow Matching to model per-token conditional distributions in continuous space—providing a more efficient alternative to full-frame diffusion. Finally, the decoder reconstructs the full physical trajectory from the generated latents.
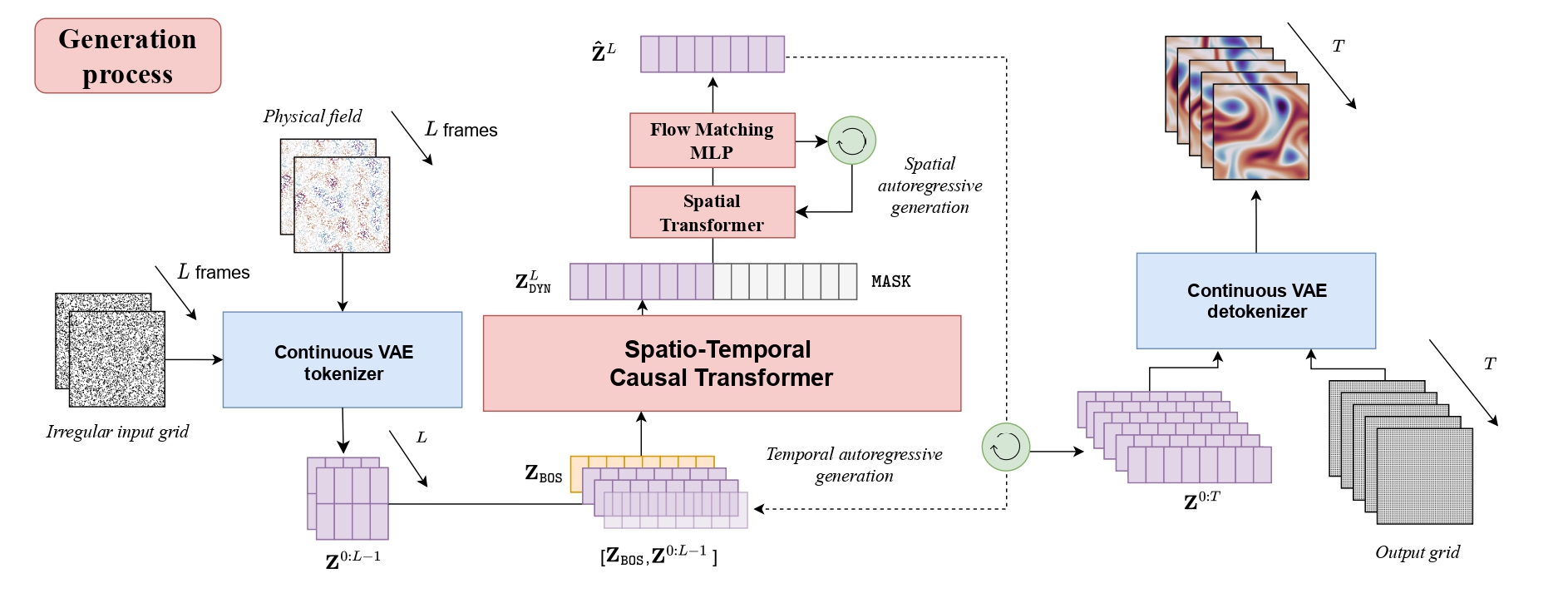
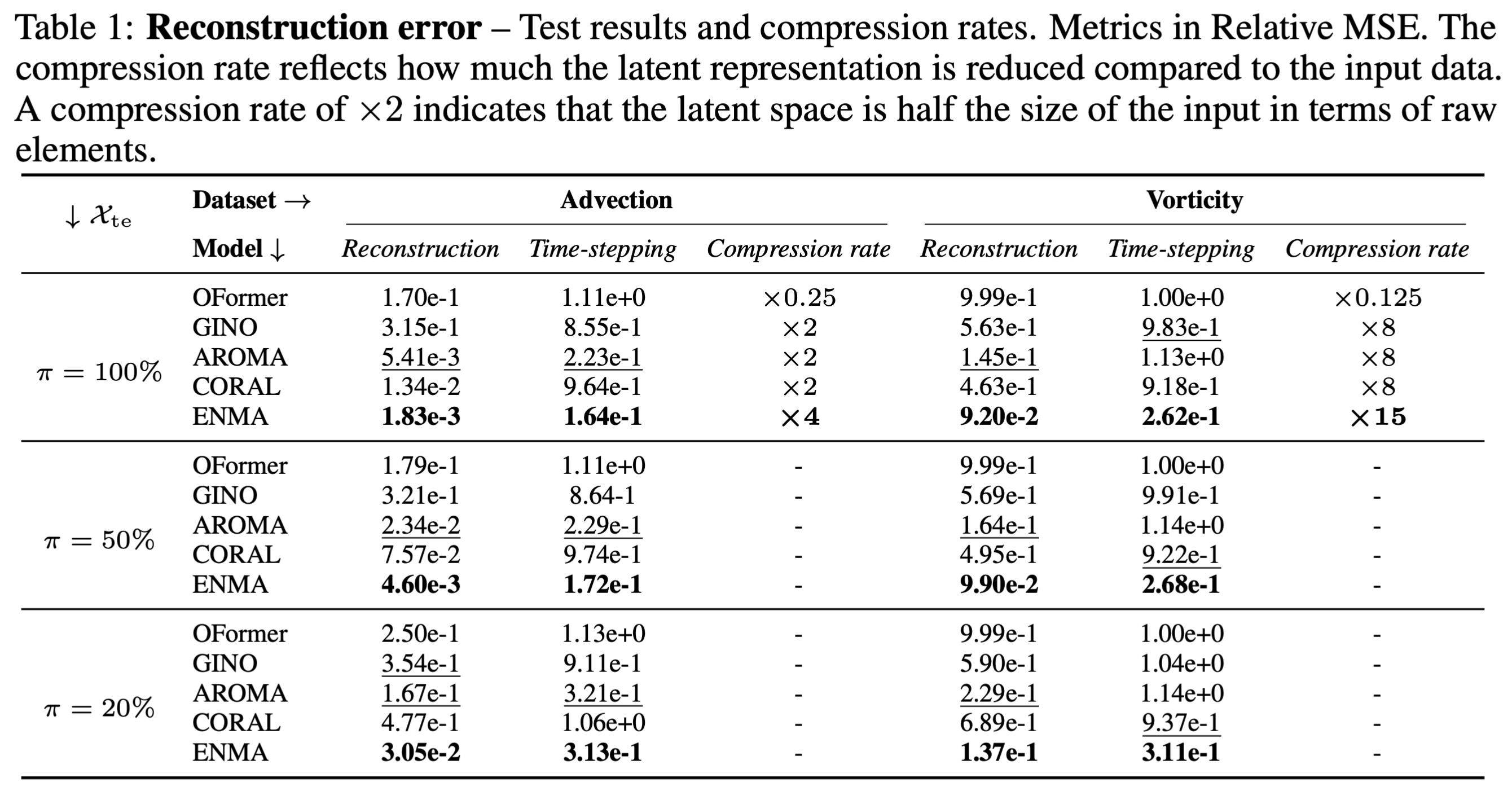
We evaluate the proposed method on several baselines and datasets to illustrate the benefits of our method. First, we show the results of the tokenwize generation process, and then, we show a comparison of our auto-encoding strategy with baselines.

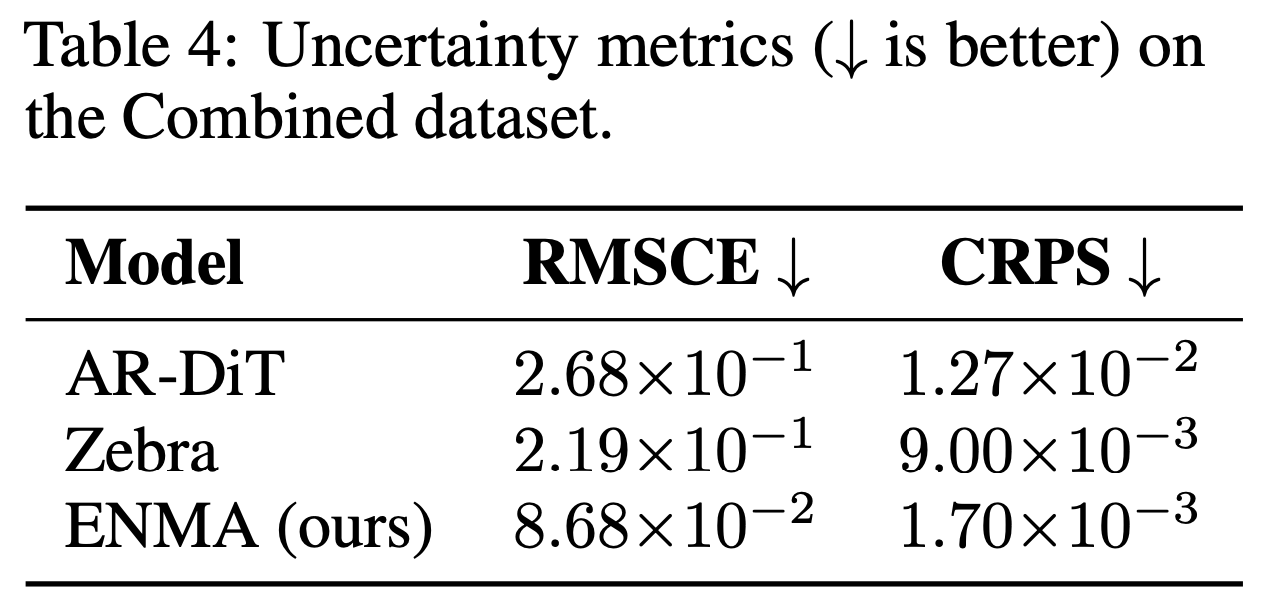
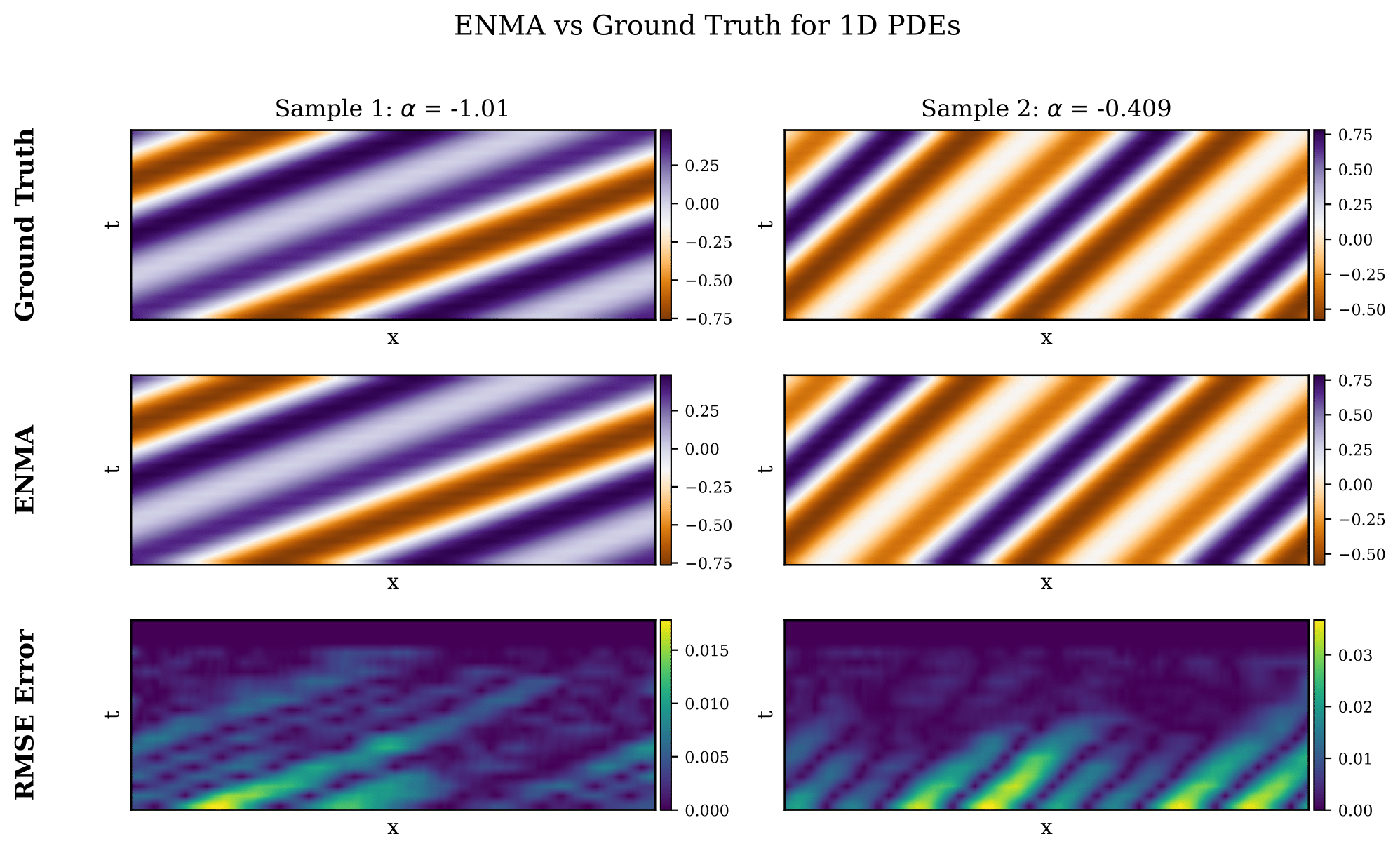
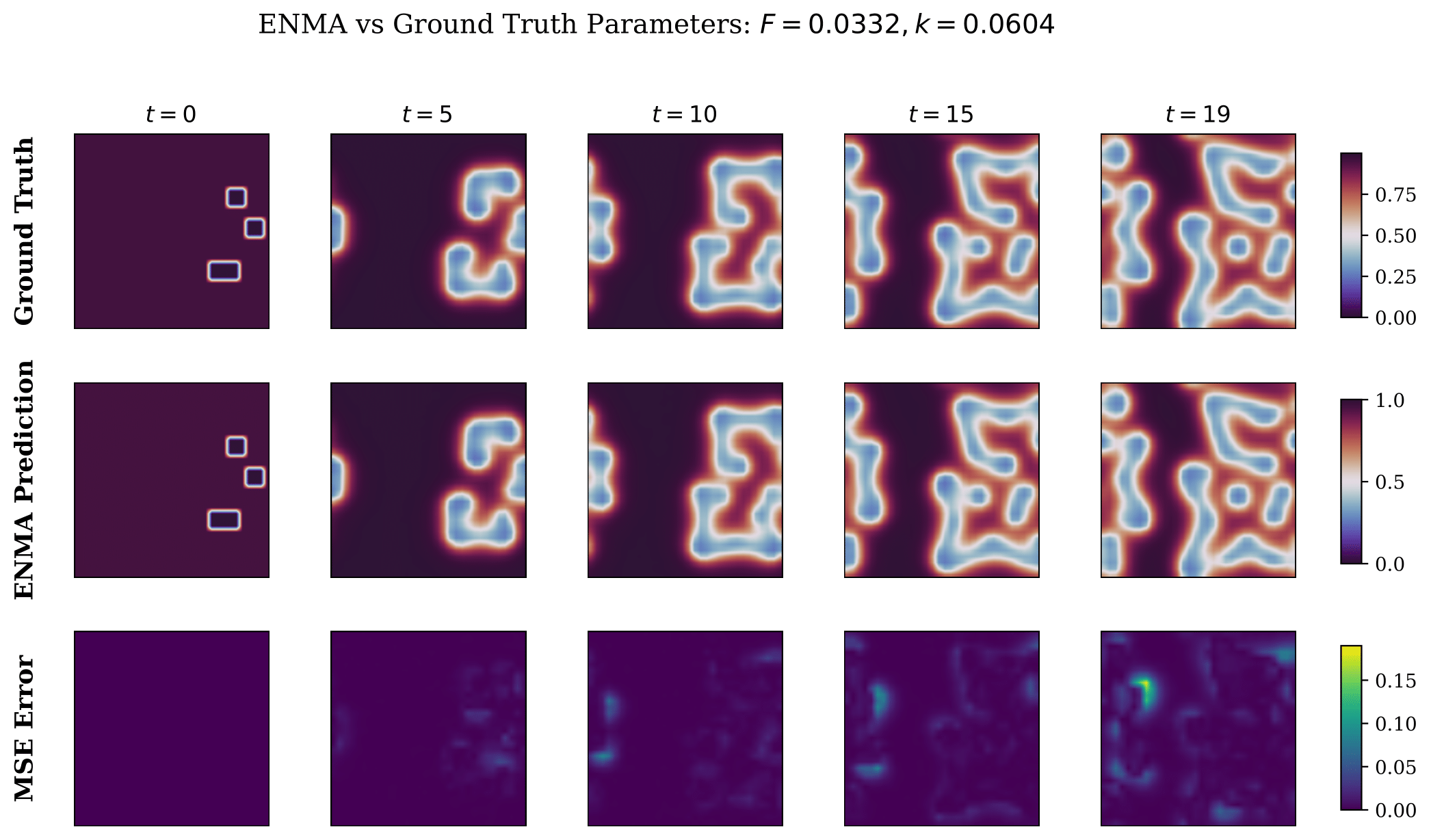
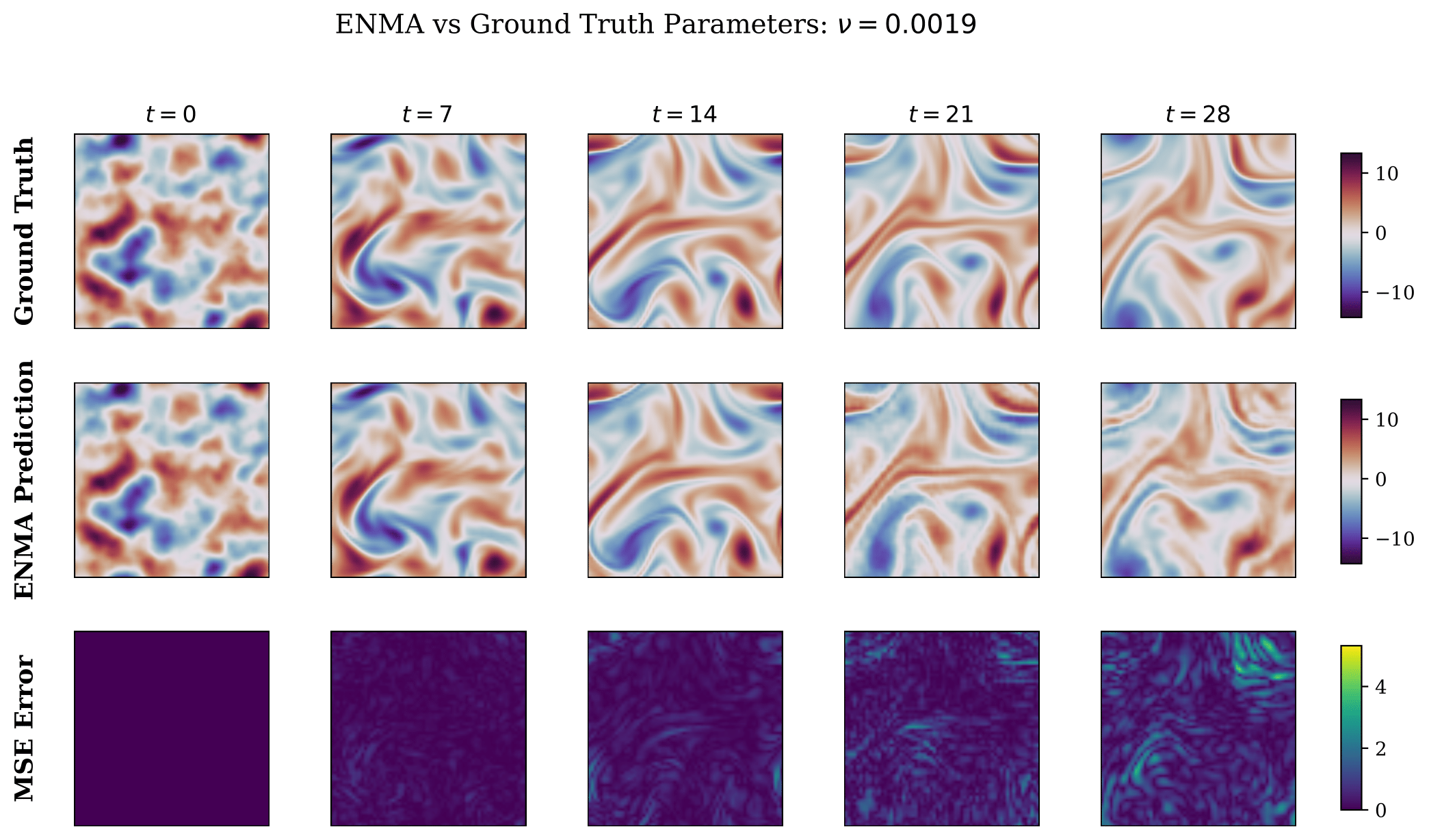
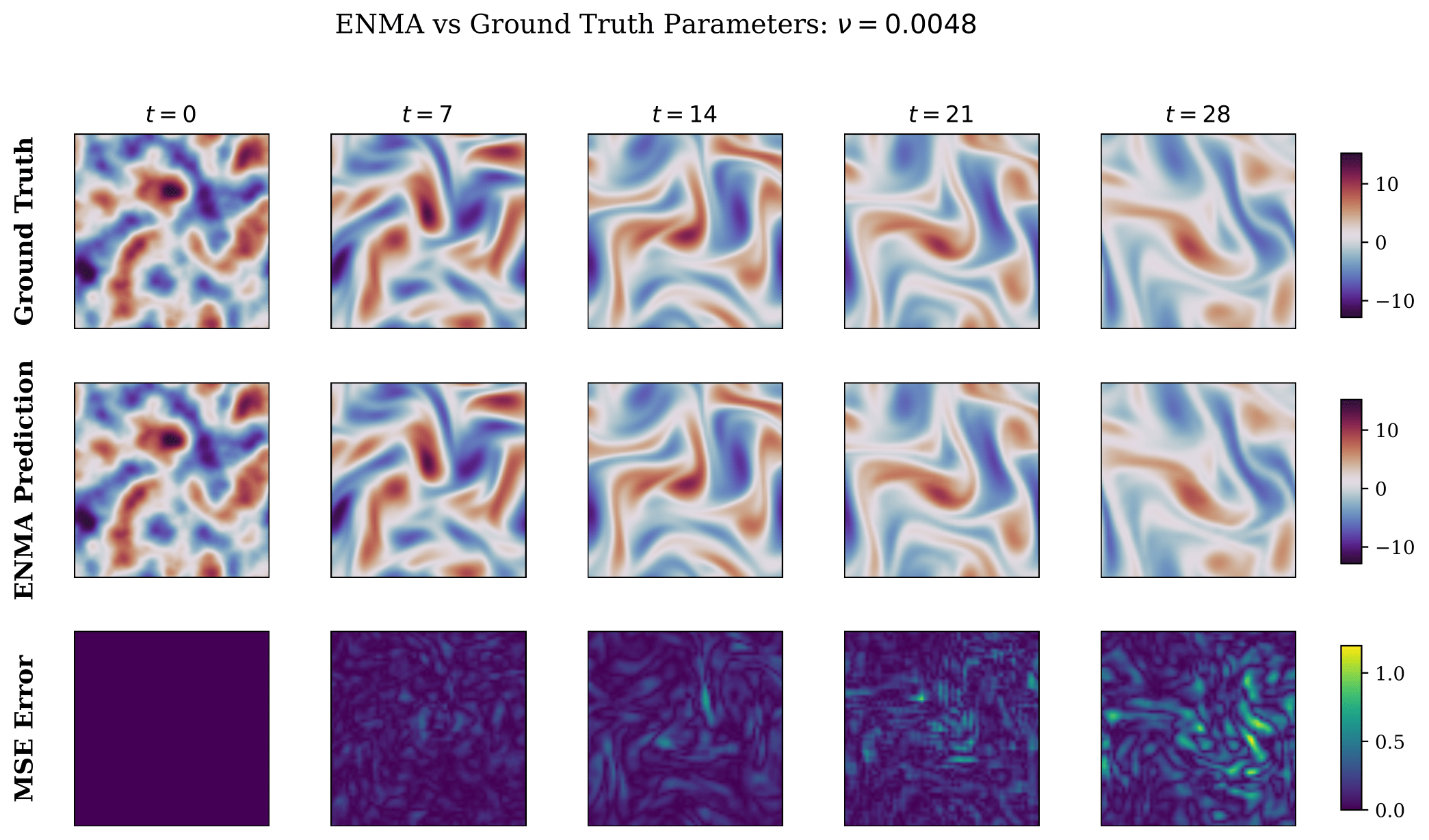
ENMA functions as a generative neural operator capable of producing stochastic and physically consistent trajectories. We highlight two core experiments that demonstrate its generative ability: an uncertainty quantification s ENMA performs uncertainty estimation by sampling multiple trajectories from its continuous latent space through stochastic flow matching.
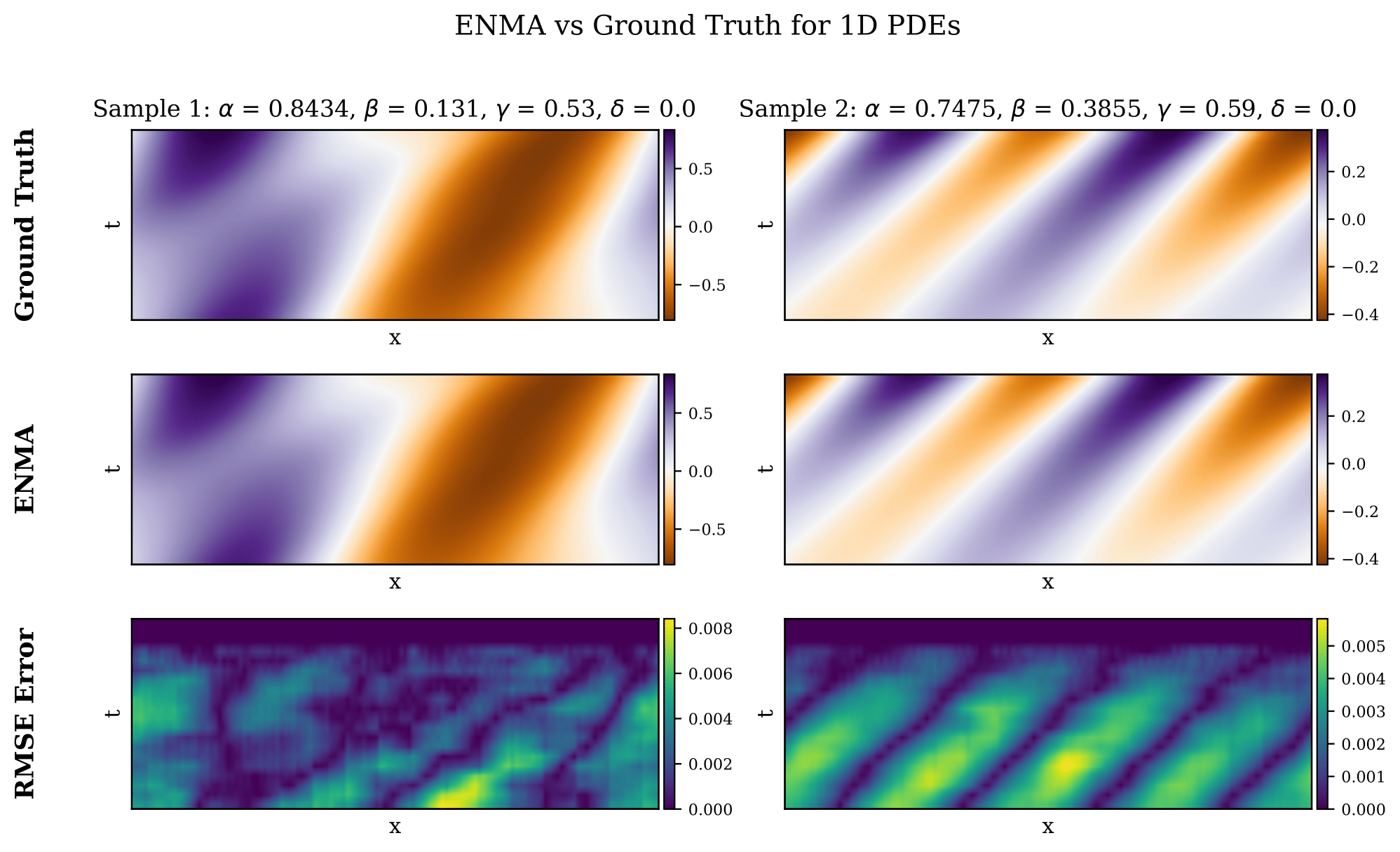
We further assess ENMA’s ability to generate full trajectories without conditioning on the initial state or PDE parameters. Given only a context trajectory, ENMA infers the latent physics and synthesizes coherent spatio-temporal fields




@inproceedings{
koupai2025enma,
title={{ENMA}: Tokenwise Autoregression for Continuous Neural {PDE} Operators},
author={Armand Kassa{\"\i} Koupa{\"\i} and Lise Le Boudec and Louis Serrano and Patrick Gallinari},
booktitle={The Thirty-ninth Annual Conference on Neural Information Processing Systems},
year={2025},
url={https://openreview.net/forum?id=3CYXSMFv55}
}